I have derived the following information from work on 'Odd and Even Functions.' It bothered me that we could not find whether a graph was symmetrical about a vertical axis other than the y-axis (x = 0) or symmetrical about a point other than the origin (0, 0). To alleviate this issue I deduced two formulae for finding firstly, whether a graph had a single source of symmetry (a point or line), and secondly, what that source was.
The first involves considering the movement of an axes of symmetry from that which even functions are defined upon, ie. x= 0; the y-axis. An axes of symmetry at x = a, is a units from x = 0, and thus all equal values for f(x) are shifted a units from the origin. An even function is defined for:
f(-x) = f(x)
Thus:
If f(-x + a) = f(x + a), for all x > a
then f(x) has an axes of symmetry at x = a
From this we can see that the original formula involves an a value of naught, such that the axes of symmetry, as required, is at x = 0.
*For the application, see next post.
The second formula is to cater for the need to find whether a graph has a source of symmetry from a point other than the origin. Using the original formula for odd functions and the logic from above we get that:
For f(-x + a) = -f(x + a), for all x > a
the point (a, 0) is a source of symmetry
This solves the problem for movement in the horizontal plane where a represents the unit distance of the point source from the origin. In order to demonstrate the solution for movement with respect to the vertical plane, I offer these diagrams for reference:
Fig. 1 Cubic Function (x3)
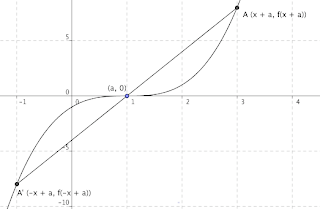
The cubic function above is an example of an odd function with rotational symmetry about the origin. The following shows the same function moved horizontally by a units.
ie. (-x + a)3 = -(x + a)3
Fig. 2 Cubic function moved horizontally
As the graph shows, the axis of symmetry lies at (a, 0). Proof of this is that (a, 0) lies on the line AA', which represents two symmetrical points that satisfy the formula g(-x + a) = -g(x + a).
Finally, this diagram shows the graph raised by b units. ie h(x) = g(x) +b.
Fig. 3 Cubic function moved vertically and horizontally
As seen above, raising the graph, and hence the source of rotational symmetry, by b units will also raise all y values and therefore, the value of the function at those points corresponding to x values > a will increase by b units and those < a will also increase by b units. This means that when making symmetrical points equal, those for which x < 0 will have an absolute value of 2b units less than the corresponding y-values for x > a. This leads to the conclusion that:
Where h(x + a) = |h(-x + a)| + 2b, for all x ≥ a, x ≠ 0 and a ≥ 0
h(x) has symmetry about the point (a, b)
OR
Where h(x + a) = |h(-x + a)| + 2b, for all x ≤ a, x ≠ 0 and a ≤ 0
h(x) has symmetry about the point (a, b)


No comments:
Post a Comment